LS-DYNA引入不可壓縮光滑粒子伽遼金方法ISPG,以拉格朗日方式求解納維-斯托克斯方程�����。本方法旨在解決強(qiáng)形式拉格朗日粒子法在求解不可壓縮自由表面流動(dòng)時(shí)關(guān)鍵的數(shù)值不穩(wěn)定性問題���。ISPG方法提供了一種穩(wěn)健和有效的方法求解精確的結(jié)果�,包括流固耦合�����。
回流焊工藝涉及多個(gè)設(shè)計(jì)因素���,這些因素能夠影響熔融焊點(diǎn)的結(jié)果形狀�����,如焊點(diǎn)體積�����、恢復(fù)力��、表面張力��、接觸角����、焊盤厚度和焊盤尺寸等����,采用ISPG方法進(jìn)行模擬時(shí)能將這些因素都考慮在內(nèi)。使用基于節(jié)點(diǎn)云的網(wǎng)格重劃分和節(jié)點(diǎn)刪除與插入的算法用于處理焊料拓?fù)湫螤畹淖兓?����,包括焊料橋接和焊料分離以及非常復(fù)雜的邊界條件����,比如尖角。仿真計(jì)算結(jié)果與理論分析結(jié)果吻合較好���,表明該方法可用于SMD/NSMD焊點(diǎn)回流形狀的預(yù)測(cè)����。該研究為設(shè)計(jì)人員準(zhǔn)確預(yù)測(cè)回流焊過程中焊點(diǎn)的液體形成提供了基本指導(dǎo)�����。同時(shí),近期自適應(yīng)ISPG方法在各種粘接接頭和涂層問題中的粘膠流動(dòng)模擬中的同樣有著成功的應(yīng)用案例��。本文將主要介紹:
ISPG方法的通用介紹及在回流焊中的應(yīng)用
自適應(yīng)ISPG方法的新發(fā)展
回流焊應(yīng)用案例
基于自適應(yīng)ISPG方法進(jìn)行粘膠流動(dòng)和涂層模擬
總結(jié)����、當(dāng)前研發(fā)進(jìn)展以及Mechanical界面的ISPG插件
對(duì)于顯式求解器來(lái)說,不可壓流體計(jì)算由于受材料體積模量的限制���,時(shí)間步長(zhǎng)非常小��,帶來(lái)巨大的計(jì)算量�,即使模擬1~2秒工況問題��,也需要耗費(fèi)幾天甚至十幾天的計(jì)算時(shí)間��。而隱式算法則可以避免這類不足����,其時(shí)間步長(zhǎng)可以較大�,計(jì)算效率顯著提高�,相對(duì)于顯式在不可壓縮流體計(jì)算方面有著巨大的優(yōu)勢(shì)。雖然ISPG方法更偏向于是一種基于粒子的伽遼金方法�����,但它仍然需要借助網(wǎng)格來(lái)積分��,而流體的變形往往會(huì)非常的大���,若網(wǎng)格的變形太大,很多問題也無(wú)法進(jìn)行計(jì)算���。因此LS-DYNA研發(fā)了一種新的方法:自適應(yīng)網(wǎng)格更新ISPG方法�,該方法種網(wǎng)格會(huì)持續(xù)不停的更新�,形成非常規(guī)則的網(wǎng)格,從而能夠?qū)崿F(xiàn)隱式求解時(shí)更快的迭代速度及更高的效率��。大變形問題中若網(wǎng)格不能及時(shí)更新�����,很可能出現(xiàn)不收斂等情況��。
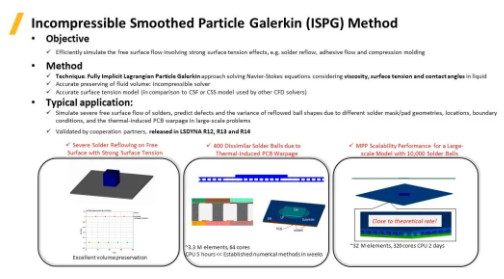
ISPG的全稱為Incompressible Smoothed Particle Galerkin Method不可壓縮光滑粒子伽遼金法,是完全的隱式計(jì)算方法�。ISPG可有效地求解涉及強(qiáng)表面張力效應(yīng)的自由表面流動(dòng)問題,如回流焊���,粘膠流動(dòng)和壓縮成形等�����。ISPG基于完全隱式拉格朗日粒子伽遼金方法求解考慮液體粘度��、表面張力和接觸角的Navier-Stokes方程��,可精確地保持流體體積�,能夠精確地模擬回流焊過程中焊球形狀形成的過程(考慮自由表面流�、表面張力和附著力),研究回流焊工藝過程中可能出現(xiàn)的缺陷����,如翹曲、橋接和虛焊等����。
上圖中左一案例為具有強(qiáng)表面張力的自由表面的回流焊模擬,焊球在溫度影響下逐漸展現(xiàn)流體的性質(zhì)�,在接觸壁面時(shí)��,其表面在表面附著力的作用下擴(kuò)張�,形成非常大的變形�����。由于使用的是不可壓的流體求解器���,模擬過程中焊球的體積變化幾乎為零,說明ISPG方法在保持體積方面表現(xiàn)非常優(yōu)秀�。中間案例為由于熱膨脹引起PCB電路板翹曲中回流焊焊接的過程,在流體表面施加邊界條件進(jìn)行流固耦合計(jì)算�,模擬過程精確預(yù)測(cè)了每個(gè)焊球的變形過程。右一案例顯示了具有10,000個(gè)焊球的大型模型���,該模型包含3200萬(wàn)單元并使用320核CPU��,基于全隱式計(jì)算�,計(jì)算在2天內(nèi)完成���,展示了LS-DYNA ISPG計(jì)算大規(guī)模模型的強(qiáng)大能力����。
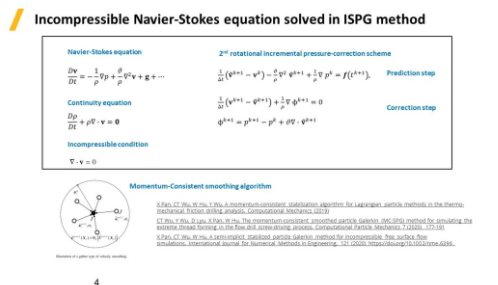
ISPG方法的基本理論�。作為一種流體求解器,ISPG以拉格朗日方式求解Navier-Stokes方程���,同時(shí)加入流體的連續(xù)性方程和不可壓縮條件�����,通過動(dòng)量守恒光滑算法�,基于隱式求解得到相對(duì)應(yīng)的壓力����、速度和位移。感興趣的用戶可以參考以下三篇論文:
X Pan, CT Wu, W Hu, Y Wu, A momentum-consistent stabilization algorithm for Lagrangian particle methods in the thermo-mechanical friction drilling analysis, Computational Mechanics (2019)
CT Wu, Y Wu, D Lyu, X Pan, W Hu, The momentum-consistent smoothed particle Galerkin (MC-SPG) method for simulating the extreme thread forming in the flow drill screw-driving process, Computational Particle Mechanics 7 (2020) 177-191
X Pan, CT Wu, W Hu, A semi-implicit stabilized particle Galerkin method for incompressible free surface flow simulations, International Journal for Numerical Methods in Engineering, 121 (2020) https://doi.org/10.1002/nme.6396

回流焊過程包含大量復(fù)雜的物理現(xiàn)象如:翹曲����、自由表面流動(dòng)�、強(qiáng)表面張力�、壁面粘附�、熱相關(guān)、流體熔合(分離)����、相變等。而常規(guī)歐拉方法Eulerian在自由表面流動(dòng)模擬中的困難主要表現(xiàn)為:
而ISPG方法是一種拉格朗日方法,顆粒隨著材料變形運(yùn)動(dòng)����,材料變形的表面即為顆粒的表面��,更適合流體邊界的求解以及流固耦合的模擬過程���。
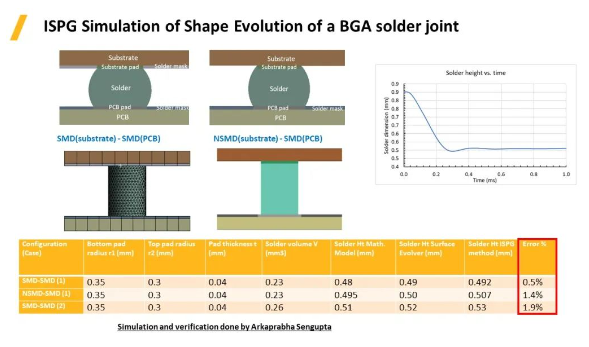
回流焊的過程通常有兩種方式:SMD(Solder Mask Defined防焊限定焊墊,其基質(zhì)上有一層阻焊層:防焊綠油/綠漆(Solder-Mask以及NSMD (Non-Solder Mask Defined非防焊限定焊墊�����,又稱銅箔獨(dú)立焊墊)�����。
如案例所示���,在基板上施加重力�����,部件向下移動(dòng)過程中焊球在表面張力作用下形成一個(gè)向上托力��,焊球高度在變化過程中有一段震動(dòng)后達(dá)到平衡�,隨后測(cè)量基板與PCB兩個(gè)面之間的距離來(lái)得出焊球的高度�����,與理論值進(jìn)行對(duì)比�����,根據(jù)圖中表格可以看出三組數(shù)據(jù)的誤差都在2%之內(nèi),體現(xiàn)了超高的精度值���。
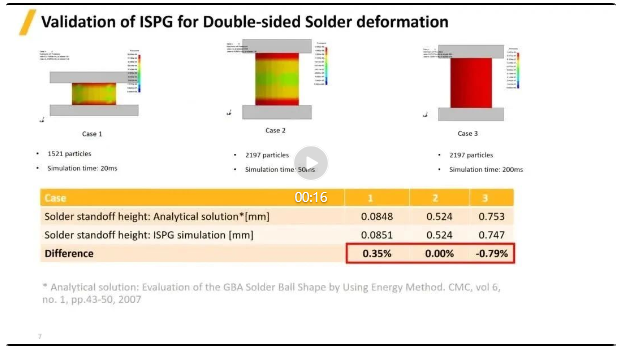
點(diǎn)擊圖片即可跳轉(zhuǎn)原文觀看視頻
上圖案例展示了另外一個(gè)驗(yàn)證過程,不同尺寸和重量的焊球在雙層板擠壓下����,由于表面張力的作用形成的結(jié)果變形形狀,結(jié)果表明精度非常高��,誤差小于1%���。
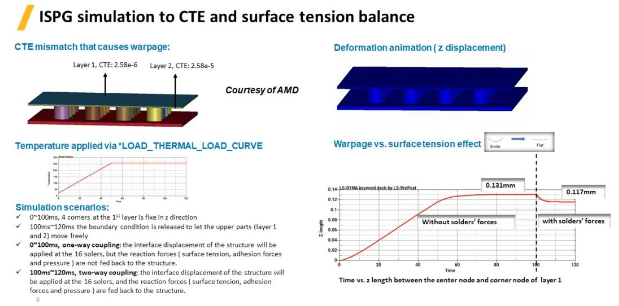
下面是一個(gè)PCB翹曲變形與焊球表面張力平衡的案例。由于不同層級(jí)電路板之間的熱膨脹系數(shù)不一致����,從而整體形成翹曲����。通過關(guān)鍵字*LOAD_THERMAL_LOAD_CURVE對(duì)上面兩個(gè)板層施加溫度載荷�,且溫度場(chǎng)隨著時(shí)間變化而變化。0~100ms�,第 一層4個(gè)角在z方向固定約束;100~120ms釋放邊界條件����,讓上部(第1層和第2層)自由移動(dòng)。在0~100毫秒之間����,進(jìn)行單向耦合仿真,16個(gè)焊球的變形會(huì)受到邊界位移的影響�����,但PCB結(jié)構(gòu)的翹曲變形不會(huì)受到焊球反作用力的影響(表面張力�����、附著力和壓力)��。而在100~120毫秒之間實(shí)行雙向耦合:既會(huì)將界面的邊界位移施加給焊球,同時(shí)也會(huì)將反作用力(表面張力��、附著力和壓力)反饋給結(jié)構(gòu)���,從而考慮焊球表面張力對(duì)PCB結(jié)構(gòu)的反作用力的影響���,動(dòng)畫中可以看到焊球的變形更加平滑。
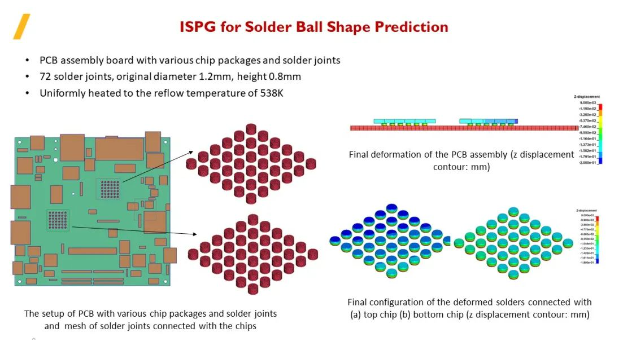
ISPG用于焊球形狀預(yù)測(cè)�。左圖為一個(gè)包含不同芯片封裝PCB板模型,芯片和電路板之間用焊球連接���。兩塊區(qū)域包含72個(gè)焊球�,每個(gè)焊球原始直徑1.2mm�����,高度0.8mm���。將整個(gè)模型均勻回流加熱至538K�,觀察回流焊過程中焊球的變形��。右上圖為PCB組件結(jié)果變形(z位移輪廓:mm)�;右下圖為(a)頂部芯片(b)底部芯片(z位移輪廓:mm)連接變形焊料的結(jié)果形態(tài)。
點(diǎn)擊圖片即可跳轉(zhuǎn)原文觀看視頻
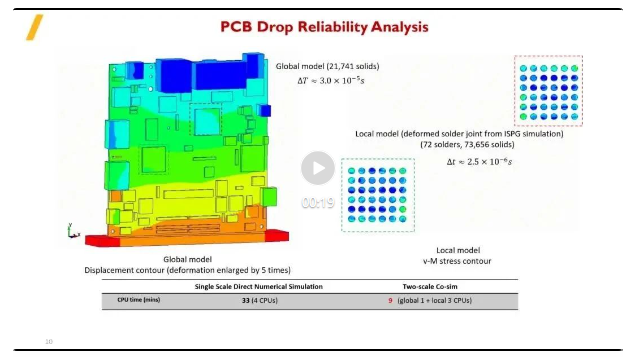
PCB跌落可靠性分析��,將焊球結(jié)果的變形形態(tài)�����,導(dǎo)入整體電路板跌落模型中���,通過對(duì)比單尺度直接數(shù)值模擬與雙重尺度聯(lián)合仿真,研究焊球在跌落過程中對(duì)整體部件的影響����。
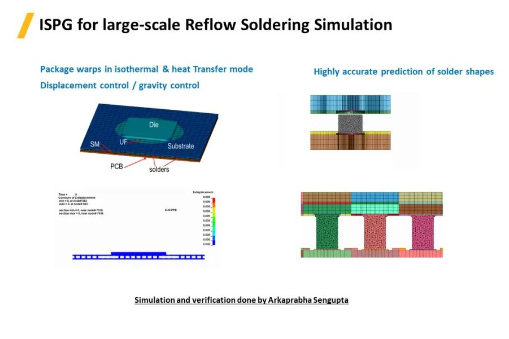
ISPG應(yīng)用于大規(guī)模回流焊模擬過程����。封裝過程中PCB板常常會(huì)發(fā)生翹曲,焊球在重力載荷和邊界位移條件的作用下發(fā)生變形�����,實(shí)驗(yàn)表明模擬過程ISPG方法精準(zhǔn)的預(yù)測(cè)到了每個(gè)焊球的變形����。

利用ISPG進(jìn)行簡(jiǎn)化封裝模型的焊接組裝過程仿真���,封裝和PCB用簡(jiǎn)化的方塊表示����,模擬過程包含三個(gè)步驟:將模具基質(zhì)加熱到205℃,然后進(jìn)行焊接���,然后冷卻到150℃。100個(gè)焊點(diǎn)的模型(包含15.2萬(wàn)個(gè)節(jié)點(diǎn))采用10個(gè)CPU計(jì)算,運(yùn)行時(shí)間為2.5小時(shí);若采用64個(gè)CPU運(yùn)算1,225個(gè)焊點(diǎn)(包含102萬(wàn)個(gè)節(jié)點(diǎn))的類似模型����,則僅耗時(shí)7.6小時(shí),在確保精度的前提下�,計(jì)算效率非常高��。
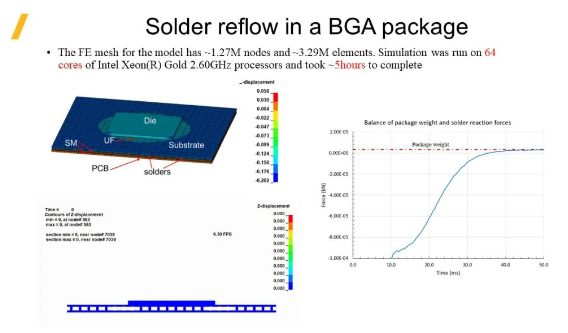
BGA封裝中的回流焊,模型相對(duì)更復(fù)雜��,其包含有限元網(wǎng)格節(jié)點(diǎn)數(shù)約為127萬(wàn)���,單元數(shù)約為329萬(wàn)�����。在64核Intel Xeon(R) Gold 2.60GHz CPU上運(yùn)行計(jì)算���,耗時(shí)約5小時(shí)�。右側(cè)圖表可以看到在該模型變形過程中�����,焊球頂端對(duì)上板的作用力趨于某個(gè)平衡點(diǎn)的過程�,并且這個(gè)作用力與上板的重量一致。從這點(diǎn)也可以證明�����,ISPG方法的精度之高�����。
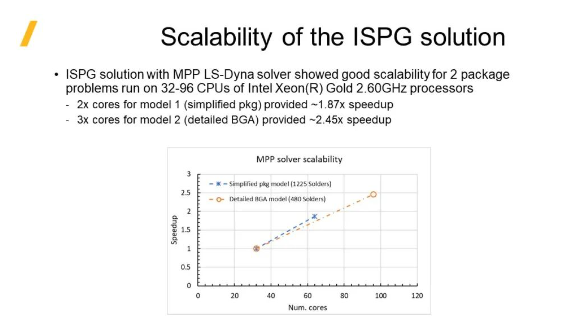
ISPG方法良好的可擴(kuò)展性�����。在Intel Xeon(R) Gold 2.60GHz CPU的32-96個(gè)CPU上計(jì)算�, 采用LS-DYNA MPP版本的ISPG方法顯示出良好的可擴(kuò)展性:

10,000個(gè)回流焊模擬的效率測(cè)試���,模型采用10,000個(gè)焊球總共包含17,187,605個(gè)節(jié)點(diǎn)和32,303,312個(gè)單元��,160個(gè)CPU運(yùn)行時(shí)間為91小時(shí)���;320 個(gè)CPU運(yùn)行時(shí)間為55小時(shí),比采用160 CPU快1.7倍�,并行加速的可擴(kuò)展性非常好。

當(dāng)計(jì)算中需要模擬的物理幾何形狀及邊界條件非常復(fù)雜時(shí)(比如尖角等),若沒有網(wǎng)格更新�,尖角的地方很難完全貼合,可能存在間隙及穿透現(xiàn)象�����。在焊球的橋接過程中���,也需要網(wǎng)格不斷地更新����。因此���,我們需要網(wǎng)格自動(dòng)更新的自適應(yīng)ISPG方法�。
ISPG實(shí)現(xiàn)了新的基于in-core的網(wǎng)格自適應(yīng)框架����,網(wǎng)格重劃分的過程無(wú)需重啟動(dòng)計(jì)算
與LS-PrePost團(tuán)隊(duì)合作完成對(duì)自適應(yīng)ISPG d3plot結(jié)果后處理的支持
基于節(jié)點(diǎn)云的自適應(yīng)算法
新的ISPG -流固耦合算法
1)、使流體與固體面完全對(duì)齊�����,解決穿透問題
2)、根據(jù)結(jié)構(gòu)面段特征自動(dòng)調(diào)整顆粒分布�����,顯著減少達(dá)到理想精度所需的節(jié)點(diǎn)數(shù)(用于壓縮成型和粘合劑流動(dòng))
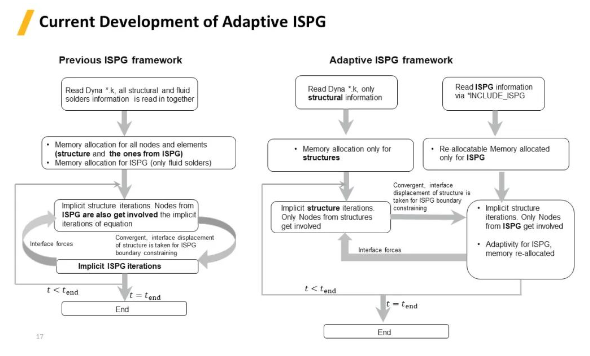
總體來(lái)說���,原來(lái)的ISPG工作流程是將流體與固體的模型放在同一個(gè)文件里��,并使用同一個(gè)迭代算法隱式求解���,流固耦合計(jì)算中將固體表面作為邊界�����,然后通過流體對(duì)固體的作用力反饋到固體表面����。而自適應(yīng)ISPG方法中流體跟固體模型完全分開��,流體模型通過*INCLUDE_ISPG讀取�,并在內(nèi)部形成獨(dú)立的求解過程,流固耦合計(jì)算時(shí)�,通過不同的點(diǎn)之間相互作用力以及位移來(lái)各自求解,也正是由于各自的獨(dú)立運(yùn)行�����,子循環(huán)更加容易����。
點(diǎn)擊圖片即可跳轉(zhuǎn)原文觀看視頻
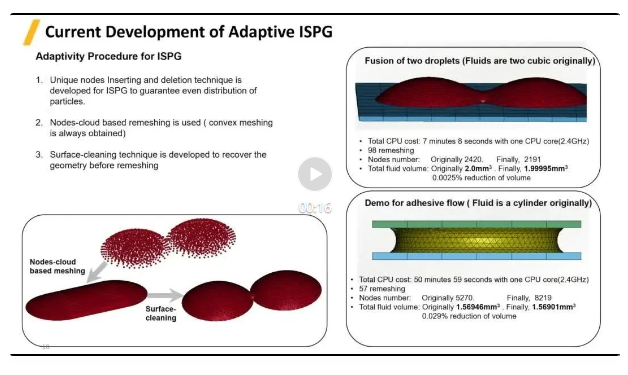
ISPG自適應(yīng)過程
ISPG特有的節(jié)點(diǎn)插入和刪除的技術(shù)可以保證重劃分后粒子的均勻分布
使用基于節(jié)點(diǎn)云的網(wǎng)格重劃分(始終得到凸面形狀的網(wǎng)格)
利用表面清理技術(shù)在網(wǎng)格重畫劃分后恢復(fù)原來(lái)的幾何形狀
右上角案例展示了兩個(gè)液滴的融合過程(流體原本是兩個(gè)立方的)���,該案例使用一個(gè)CPU(2.4GHz)計(jì)算時(shí)間7分8秒�����,包含了98個(gè)網(wǎng)格更新過程�����,節(jié)點(diǎn)數(shù)從一開始的2,420個(gè)到后面的2,191個(gè),總流體體積從2.0?mm3減少到1.99995?mm3���,減小約0.0025%��。證明網(wǎng)格更新的體積保持的效果相當(dāng)理想�����。
右下角案例展示了粘性流體受兩個(gè)板擠壓���,而沿著兩個(gè)板之間擴(kuò)張并結(jié)果溢出的過程���。擠壓過程使得粘性流體產(chǎn)生大變形成為薄薄的一層,該案例使用1個(gè)CPU (2.4GHz) 計(jì)算時(shí)間為50分鐘59秒�,包含了57個(gè)網(wǎng)格更新過程,節(jié)點(diǎn)數(shù)從一開始的5,270個(gè)到后面的8,219個(gè)���,總流體體積從1.56946 mm3減少到1.56901?mm3��,體積減小0.029%�,體積保持效果同樣表現(xiàn)優(yōu)秀����。
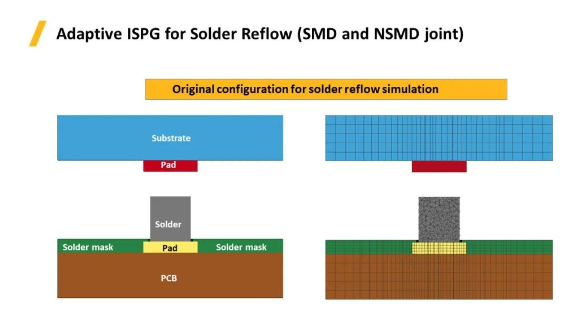
自適應(yīng)ISPG網(wǎng)格更新算法應(yīng)用于回流焊 (SMD和NSMD)模擬的過程���,案例中展示的兩個(gè)模型包含基板���,焊盤����,焊球�����,電路板和阻焊層等�����。
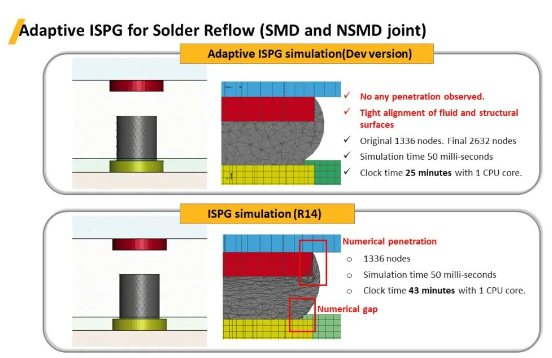
在新開發(fā)版本求解器(Dev版本)��,借助自適應(yīng)ISPG的網(wǎng)格更新功能�����,焊球與結(jié)構(gòu)邊界完全貼合����,沒有出現(xiàn)任何穿透現(xiàn)象��;且流體和固體表面緊密對(duì)齊;節(jié)點(diǎn)從原來(lái)的1,336個(gè)變化為2,632個(gè)��,模擬時(shí)間50毫秒��,1個(gè)CPU計(jì)算時(shí)間25分鐘���。
而原來(lái)的R14版本中�,使用沒有網(wǎng)格重劃分功能的ISPG�,焊球在變形過程中,在結(jié)構(gòu)尖角處出現(xiàn)了間隙和穿透的現(xiàn)象���,該過程模擬時(shí)間50毫秒�,1,336個(gè)節(jié)點(diǎn)����,1個(gè)CPU計(jì)算時(shí)間約為43分鐘。
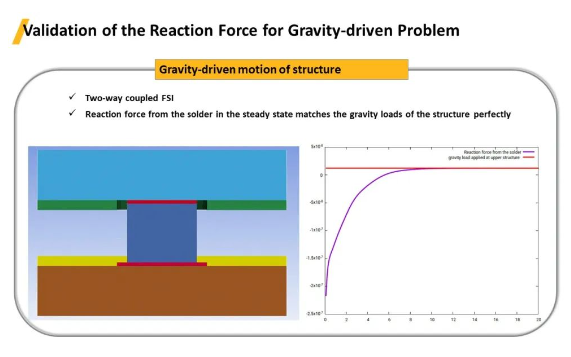
重力驅(qū)動(dòng)問題反作用力的驗(yàn)證����。重力驅(qū)動(dòng)的結(jié)構(gòu)運(yùn)動(dòng)為雙向耦合FSI,將流固耦合過程中流體反饋給固體邊界的作用力讀取出來(lái)(右圖圖表)���,該作用力會(huì)穩(wěn)定趨于一個(gè)數(shù)值平衡點(diǎn)�,穩(wěn)定狀態(tài)下焊球的反作用力與結(jié)構(gòu)的重力載荷完全吻合。
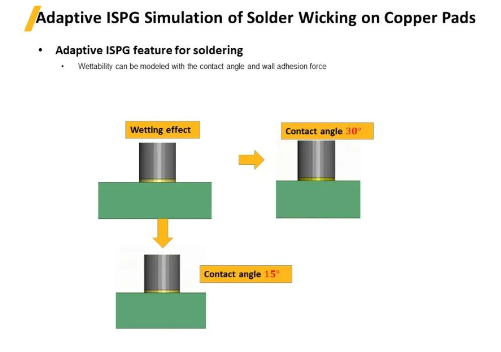
自適應(yīng)ISPG模擬銅焊盤爬錫過程。潤(rùn)濕性可以用接觸角和壁面附著力來(lái)建模���。圖中展示了定了不同接觸角的吸錫過程模擬案例�����。接觸角15°的模型����,其潤(rùn)濕性明顯比接觸角30°的模型更好��。
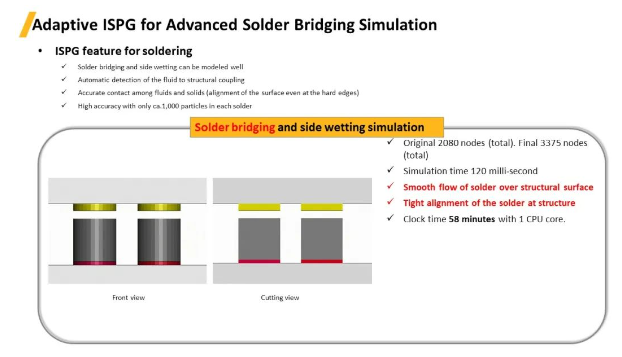
上圖案例中展示了焊球橋接過程的模擬�����,當(dāng)算法檢測(cè)到當(dāng)兩個(gè)焊球的間隙足夠近時(shí)��,將其融合成一個(gè)焊球���。
可以很好地模擬焊球橋接和側(cè)面潤(rùn)濕
自動(dòng)探測(cè)流體和固體之間的耦合關(guān)系
流體和固體之間的精確接觸(即使在硬邊緣處表面也能對(duì)齊)
高精度�,每個(gè)焊球中只有約1,000個(gè)粒子
初始節(jié)點(diǎn)總數(shù)2,080個(gè)���,結(jié)果變?yōu)?,375個(gè)
模擬時(shí)間120毫秒
焊球在結(jié)構(gòu)表面的平滑流動(dòng)
焊球在結(jié)構(gòu)上的緊密貼合
1個(gè)CPU計(jì)算時(shí)間58分鐘
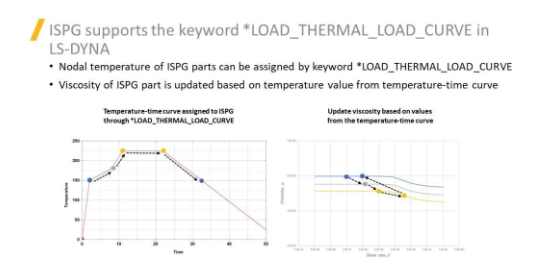
LS-DYNA ISPG方法支持*LOAD_THERMAL_LOAD_CURVE關(guān)鍵字�����,通過該關(guān)鍵字指定部件的節(jié)點(diǎn)溫度�����,在模擬回流焊過程中施加持續(xù)的溫度載荷(隨著時(shí)間變化)��。同時(shí),可將ISPG部件的粘度定義為溫度的函數(shù)��,根據(jù)溫度-時(shí)間曲線的溫度值更新流體的粘度��。
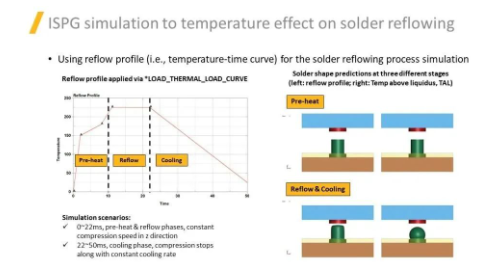
ISPG模擬溫度對(duì)回流焊的影響��,使用回流曲線定義過程中溫度隨時(shí)間的變化��。模擬場(chǎng)景:
應(yīng)用案例-粘膠劑流動(dòng)��、涂層模擬
背景:膠粘劑在鋁���、碳纖維����、鋼等不同材料零部件的連接中的作用越來(lái)越大。
膠粘劑的表面張力��、表面吸附力以及非牛頓流體特性對(duì)膠粘劑的流動(dòng)至關(guān)重要���。目前ISPG研發(fā)的內(nèi)容包括非牛頓流體模型�,考慮流體性質(zhì)隨時(shí)間和溫度變化的效應(yīng)���,如流凝性流體���、觸變性流體、Bingham流體以及 Hershel-bulkley流體等�����。

目前ISPG支持三種流體粘度定義選項(xiàng):
牛頓粘性(即恒定粘性)
非牛頓粘性
與溫度相關(guān)的粘性
ISPG支持LS-DYNA中*LOAD_THERMAL_LOAD_CURVE關(guān)鍵字對(duì)ISPG部件進(jìn)行節(jié)點(diǎn)溫度分配�����。

上圖展示了使用ISPG進(jìn)行薄膜涂層的分析案例,圖中使用了軸對(duì)稱的模型��。涂層粘性流體初始高度0.1毫米���,半徑0.5毫米����,設(shè)置接觸角為0.1度����??梢钥吹?��,由于接觸角非常的小���,流體在表面吸附力作用下表面擴(kuò)張成薄薄的一層,結(jié)果厚度0.00337毫米��,半徑是3.85毫米���,厚度與半徑之比非常小。模擬值與理論值誤差小于0.2%�,由此可以說明ISPG模擬精度非常高。
ISPG可以用非常粗的網(wǎng)格(原來(lái)是z方向的一層單元)精確地預(yù)測(cè)受微小接觸角(甚至0.1°)影響的流體分布���,在薄膜涂層模擬中具有很好的應(yīng)用前景����。
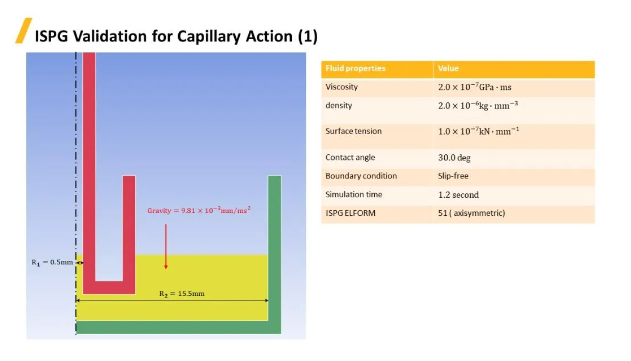
ISPG進(jìn)行毛細(xì)管的仿真��,這同樣是一個(gè)軸對(duì)稱的模型����。內(nèi)外兩個(gè)容器�����,內(nèi)容器半徑0.5毫米�,外容器半徑15.5毫米�����,液體在細(xì)管狀物體內(nèi)側(cè)����,在表面張力和壁面吸附力的作用下,液體沿著壁面上升�,結(jié)果整體形成凹面的形狀。

將仿真得到的極高點(diǎn)壓力和液體高度與理論值做比較�����,誤差均在1%以內(nèi),精度表現(xiàn)十分理想�����。
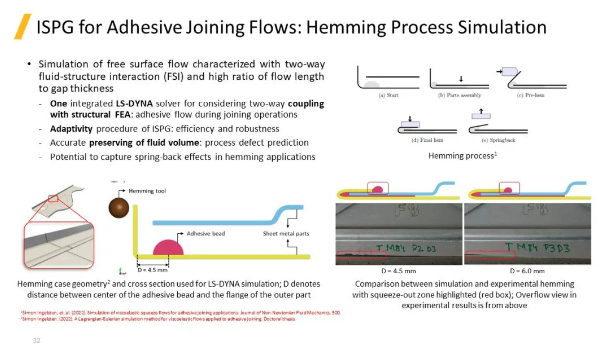
上圖是使用ISPG模擬包邊工藝過程中的粘膠劑流動(dòng)過程的案例���。這是一個(gè)自由表面流動(dòng)問題�,需要考慮雙向流固耦合��,同時(shí)流動(dòng)長(zhǎng)度與間隙厚度比例較高��。
ISPG求解具有以下特點(diǎn):
LS-DYNA在一個(gè)求解器中集成多物理場(chǎng)分析能力��,能夠考慮結(jié)構(gòu)有限元與流體之間的雙向耦合�,可用于模擬零部件連接過程中的粘膠劑流動(dòng)過程
ISPG自適應(yīng)技術(shù),保證網(wǎng)格重劃分過程中的效率和穩(wěn)定性
能夠精確的保持流體的體積���,從而準(zhǔn)確的預(yù)測(cè)工藝缺陷
潛在的應(yīng)用包括捕捉包邊過程中的回彈效應(yīng)
上圖可以看到���,中間粘膠上下各有一塊金屬板材���,金屬板材往下移動(dòng)推動(dòng)粘膠沿著板材表面延展擴(kuò)張并結(jié)果溢出,粘膠厚度逐漸變薄�����。左圖展示了包變的幾何形狀和LS-DYNA模型截面示意圖�����,D為粘膠中心到包邊距離��。右側(cè)展示了仿真與實(shí)驗(yàn)的結(jié)果對(duì)比��,其中紅框中為粘膠擠出的區(qū)域���。下方為實(shí)驗(yàn)中粘膠實(shí)際溢出的結(jié)果�����。這里進(jìn)行了兩組實(shí)驗(yàn)和仿真�,分別為D=4.5mm和D=6.5mm??梢钥吹紻=6.5mm情況下粘性體擴(kuò)展的更深,溢出更少�,這與實(shí)驗(yàn)結(jié)果也是一致的。
點(diǎn)擊圖片即可跳轉(zhuǎn)原文觀看視頻
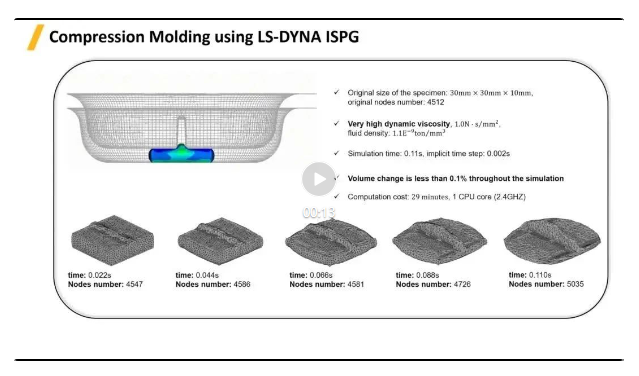
壓塑成型過程����,粘性流體在上下模擠壓作用下沿空間擴(kuò)張并成型。試件原始尺寸為30mm×30mm ×10mm��,原始節(jié)點(diǎn)數(shù)4,512個(gè)�����,流體具有非常高的動(dòng)態(tài)粘性度(1.0N?s)?m㎡ , 密度為(1.1E^(-9) ton)??mm3?����,仿真時(shí)間0.11s��,隱式時(shí)間步長(zhǎng)0.002s����,使用1個(gè)CPU (2.4GHZ)計(jì)算時(shí)間29分鐘���,整個(gè)模擬過程中體積變化小于0.1%,且擠壓過程中的流體邊界保持的非常好�����。
點(diǎn)擊圖片即可跳轉(zhuǎn)原文觀看視頻
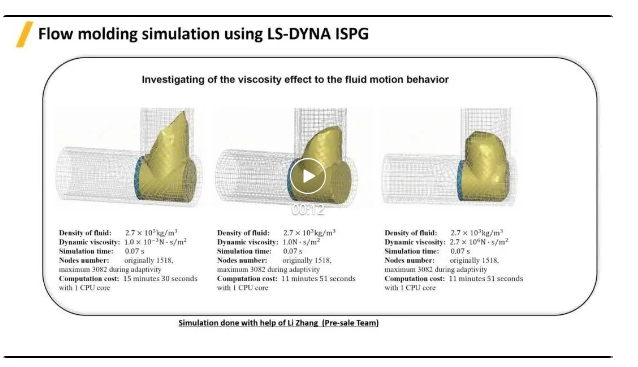
ISPG模擬流動(dòng)模塑/成型過程����,研究粘度對(duì)流體運(yùn)動(dòng)特性的影響。這里對(duì)比相同密度的粘性體在三種不同動(dòng)態(tài)粘度下運(yùn)動(dòng)過程����,仿真過程與實(shí)驗(yàn)非常接近。
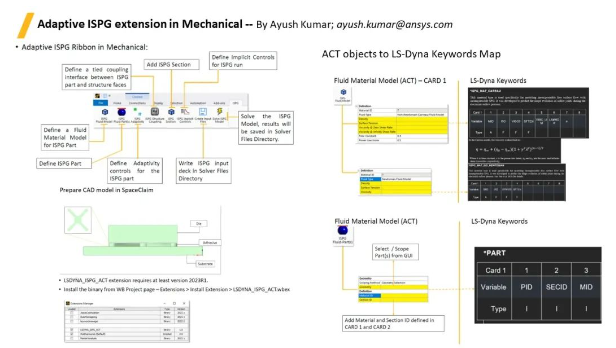

Mechanical界面中開發(fā)了用于ISPG分析的擴(kuò)展插件�����,將來(lái)用戶可以非常方便地在Mechanical界面下利用ACT進(jìn)行ISPG前后處理��。

ISPG是一種模擬自由表面流體行為的粒子方法����,可以很容易地與結(jié)構(gòu)有限元分析相結(jié)合,以準(zhǔn)確有效地求解耦合相關(guān)的問題
ISPG能夠準(zhǔn)確有效地模擬具有表面張力和壁面粘附效應(yīng)的自由表面流動(dòng)
ISPG模型可以在ANSYS Mechanical界面中進(jìn)行建模
實(shí)現(xiàn)了新的in core自適應(yīng)框架���,加快了網(wǎng)格自適應(yīng)重劃分地過程�����,并開發(fā)了基于節(jié)點(diǎn)云的ISPG自適應(yīng)算法,具備更好的穩(wěn)定性和可行性
開發(fā)了新的ISPG -結(jié)構(gòu)耦合算法�����,使流體表面與結(jié)構(gòu)表面對(duì)齊,解決了穿透問題�����。并根據(jù)結(jié)構(gòu)面段信息自動(dòng)調(diào)整粒子的分布���,大大減少了了達(dá)到理想精度所需的節(jié)點(diǎn)數(shù)���,提高了計(jì)算效率
開發(fā)了流體熔合算法,并利用該算法對(duì)焊料橋接進(jìn)行了仿真���。此外����,還包含非牛頓流體模型����,能夠模擬非牛頓粘性流動(dòng)問題
私信添加工作人員微信可獲取相關(guān)模型及學(xué)習(xí)資料
更多內(nèi)容分享,歡迎關(guān)注我們��!
相關(guān)閱讀
活動(dòng) | 使用LS-DYNA光滑粒子伽遼金(SPG)方法進(jìn)行生物材料加工過程仿真
活動(dòng)| Ansys LS-DYNA 2023R1&LS-DYNA Solver R14.0新功能介紹
活動(dòng) | LS-DYNA中自適應(yīng)ISPG方法的新進(jìn)展及其應(yīng)用--回流焊、膠粘劑流動(dòng)和涂層模擬
